Số hoàn thiện (hay còn gọi là số hoàn chỉnh, số hoàn hảo) là số nguyên dương có tổng các ước số nguyên dương bé hơn nó bằng chính nó.
Các số hoàn thiện chẵn
Euclid đã khám phá ra 4 số hoàn thiện nhỏ nhất dưới dạng: 2n−1(2n − 1):
- khi n = 2: 21(22 − 1) = 6
- khi n = 3: 22(23 − 1) = 28
- khi n = 5: 24(25 − 1) = 496
- khi n = 7: 26(27 − 1) = 8128.
Chú ý rằng: 2n − 1 đều là số nguyên tố trong mỗi ví dụ trên, Euclid chứng minh rằng công thức: 2n−1(2n − 1) sẽ cho ta một số hoàn chỉnh chẵn khi và chỉ khi 2n − 1 là số nguyên tố.
Các nhà toán học cổ đại chấp nhận đây là 4 số hoàn thiện nhỏ nhất mà họ biết, nhưng đa số những giả định trên đây đã không được chứng minh là đúng. Một trong số đó là nếu 2, 3, 5, 7 là 4 số nguyên tố đầu tiên thì nhất định sẽ có số hoàn thiên thứ 5 khi n=11, số nguyên tố thứ 5. Nhưng 211 − 1 = 2047 = 23 × 89 lại kông phải là số nguyên tố và thế là n = 11 không thu được số hoàn thiện. 2 sai lầm khác của họ là:
Số hoàn thiện thứ 5 phải có 5 chữ số theo hệ cơ số 10 vì 4 số hoàn thiện đầu tiên có lần lượt 1, 2, 3, 4 chữ số
Chữ số hàng đơn vị của Số hoàn thiện phải là 6, 8, 6, 8 và cứ thế lập lại.
Số hoàn thiện thứ 5 (33550336 = 212(213 − 1)) bao gồm 8 chữ số, vậy nhận định 1 đã sai, về nhận định thứ 2 thì số này tận cùng là 6. Tuy nhiên đến số thứ 6 (8 589 869 056) thì cũng tận cùng là 6. Nói cách khác bất cứ số hoàn thiện chẵn nào bắt buộc phải tận cùng là 6 hoặc 8.
Để 2n − 1 là số nguyên tố thì điều kiện cần nhưng chưa đủ là n nên là số nguyên tố. Số nguyên tố có dạng 2n − 1 được gọi là Số nguyên tố Mersenne sau khi được 1 nhà tu vào thế kỷ 17 là Marin Mersenne, người học lý thuyết số và số hoàn thiện tìm ra.
Hơn 1000 năm sau Euclid, Ibn al-Haytham (Alhazen) circa 1000 AD nhận ra rằng mọi số hoàn chỉnh chẵn đều phải có dạng 2n−1(2n − 1) khi 2n − 1 là số nguyên tố, nhưng ông ta không thể chứng minh được kết quả này. Mãi tới thế kỷ 18 là Leonhard Euler đã chứng minh công thức 2n−1(2n − 1) là sẽ tìm ra các số hoàn thiện chẵn. Đó là lý do dẫn tới sự liên hệ giữa số hoàn thiện và số nguyên tố Mersenne. Kết quả này thường được gọi là thuyết Euclid-Euler. Cho tới tháng 9 năm 2008, mới chỉ có 46 số Mersenne được tìm ra,[2] có nghĩa đây là số hoàn thiện số 46 được biết, số lớn nhất là 243.112.608 × (243.112.609 − 1) với 25.956.377 chữ số.
39 số hoàn thiện chẵn đầu tiên có dạng 2n−1(2n − 1) khi
- n = 2, 3, 5, 7, 13, 17, 19, 31, 61, 89, 107, 127, 521, 607, 1279, 2203, 2281, 3217, 4253, 4423, 9689, 9941, 11213, 19937, 21701, 23209, 44497, 86243, 110503, 132049, 216091, 756839, 859433, 1257787, 1398269, 2976221, 3021377, 6972593, 13466917 (sequence A000043 in OEIS)
7 số khác được biết là khi n = 20996011, 24036583, 25964951, 30402457, 32582657, 37156667, 43112609. Chưa ai biết là có để sót số nào giữa chúng hay không
Cũng chưa ai biết chắc chắn là có Vô hạn số nguyên tố Mersenne và số hoàn thiện hay không. Việc tìm ra các số nguyên tố Mersenne mới được thực hiên bởi các siêu máy tính
Bất cứ số hoàn thiện nào cũng là số tam giác và cũng giống như mọi số tam giác khác nó là tổng của tất cả các số tự nhiên cho tới số nào đó; ở đây là 2n − 1. Ngoài ra người ta nhận thấy mọi số hoàn thiện (ngoại trừ số 6) đều là tổng của 2(n−1)/2 số lẻ lập phương:
…
Ghi chú
- ^ O’Connor, John J.; Robertson, Edmund F., “Abu Ali al-Hasan ibn al-Haytham”, MacTutor History of Mathematics archive
- ^ http://www.mersenne.org/
(NGUỒN http://vi.wikipedia.org)


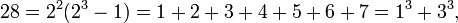
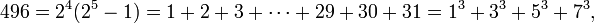
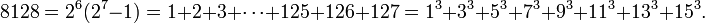
Comments are closed.