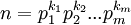Số nguyên tố – Thầy Đồ – Dạy toán

Số nguyên tố là số tự nhiên có đúng hai ước số, do vậy nó khác 0, khác 1 và chỉ chia hết cho chính nó và số một^[1]. 2 số nguyên tố đầu tiên

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Tính chất

Ký hiệu “b $\mid$ a” nghĩa là b là ước của a, ký hiệu a $\vdots$ b nghĩa là a chia hết cho b.

1. Ước tự nhiên khác 1 nhỏ nhất của một số tự nhiên là số nguyên tố .

Chứng minh: Giả sử d $\mid$ a; d nhỏ nhất; d $\ne$ 1.

Nếu d không nguyên tố $\Rightarrow$ d = d₁.d₂; d₁, d₂ > 1

$\Rightarrow$ d₁|a với d₁ < d: mâu thuẫn với d nhỏ nhất. Vậy d là nguyên tố.

2. Cho p là số nguyên tố; a $\in$ N; a $\ne$ 0. Khi đó

(a,p) = p $\Leftrightarrow$ (a $\vdots$ p)

(a,p) = 1 $\Leftrightarrow$ (a $\not\vdots$ p)

3. Nếu tích của nhiều số chia hết cho một số nguyên tố p thì có ít nhất một thừa số chia hết cho p.

$\prod_{i=1}^N a_i$ $\vdots$ p $\Rightarrow$ $\exists$ a_i $\vdots$ p

4. Ước số dương bé nhất khác 1 của một hợp số a là một số nguyên tố không vượt quá 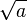$\sqrt{a}$

5. 2 là số nguyên tố nhỏ nhất và cũng là số nguyên tố chẵn duy nhất

6. Tập hợp các số nguyên tố là vô hạn (tương đương với việc không có số nguyên tố lớn nhất).

Chứng minh: Giả sử có hữu hạn số nguyên tố: p₁ < p₂ < … < p_n

Xét a = p₁.p₂. … p_{n + 1}

Ta có: a > 1 và a ¹ pi; “i = Þ a là hợp số Þ a có ước nguyên tố pi,

hay aMpi và ( pi) M pi Þ 1M pi: mâu thuẫn.

Vậy tập hợp các số nguyên tố là vô hạn.

Tuy nhiên, vì tập hợp số nguyên tố là tập con của số tự nhiên, mà tập hợp số tự nhiên là đếm được nên tập hợp các số nguyên tố là đếm được. Lưu ý khái niệm đếm được trong toán học khác với ngôn ngữ đời thường, một tập hợp có vô hạn phần tử vẫn có khả năng đếm được

Bảng số nguyên tố-sàng Eratosthene

Sàng Eratosthene

Hình minh họa cho thấy thuật toán đơn giản để tìm số nguyên tố và các bội số
Các số tô màu giống nhau là cùng một họ mà dẫn đầu (đậm hơn) sẽ là số nguyên tố

Sàng Eratosthenes là một giải thuật cổ xưa để lập bảng tất cả các số nguyên tố nhỏ hơn một số n cho trước. Giải thuật dựa trên tính chất: mọi hợp số n đều có ước nguyên tố không vượt quá căn của chính nó (sqrt(n)). Giải thuật đầu tiên xóa số 1 ra khỏi tập các số nguyên tố. Số tiếp theo số 1 là số 2, là số nguyên tố. Bắt đầu từ số 2 xoá tất cả các bội của 2 ra khỏi bảng. Số đầu tiên không bị xoá sau số 2 (số 3) là số nguyên tố. Tiếp theo lại xoá các bội của 3… Giải thuật tiếp tục cho đến khi găp số nguyên tố lớn hơn hoặc bằng sqrt(n) thì dừng lại. Tất cả các số chưa bị xoá là số nguyên tố. Theo ngôn ngữ thuật toán ta có thể diễn đạt giải thuật sàng Eratosthene như sau:

Eratosthene(n) 
 Var List Prime[1..n] 
     Int i,j,k 
 for i:=1 to n Prime[i]:=True
 Prime[1]:=false
 k=0
 while k < sqrt(n) {
    i=k+1
    while Prime[i]=False i:=i+1
    k=i
    j=2
    while k*j<=n {  
        Prime[k*j]:= False
        j:=j+1
        }
    }
   }

Lịch sử các bảng số nguyên tố

Định lý cơ bản của số học

Phát biểu định lý: “Mọi số tự nhiên lớn hơn 1 đều phân tích được thành tích những thừa số nguyên tố, và sự phân tích này là duy nhất nếu không kể đến thứ tự của các thừa số.”

Từ đó có dạng phân tích tiêu chuẩn của một số tự nhiên bất kỳ là:

$n = p_1^{k_1}p_2^{k_2}...p_m^{k_m}$

Trong đó p₁,p₂,…,p_m, là các số nguyên tố đôi một khác nhau. Ta có n chia hết cho (k₁+1)(k₂+1)…(k_m+1) số tự nhiên. Ví dụ:

300 = 2².5².3

300 chia hết cho (2+1)(2+1)(1+1)=18 số tự nhiên.

Số nguyên tố lớn nhất

Giả thiết 1: Không có số nguyên dương X nào là số nguyên tố lớn nhất, nghĩa là không tồn tại số mà các số lớn hơn nó Y > X sẽ buộc phải chia hết cho các số nguyên nhỏ hơn hoặc bằng X
Giả thiết 2: số vô cùng lớn ∞ không thể xác định là số nguyên tố hay hợp số
Giả thiết 3: Lực lượng của tập hợp số nguyên tố là vô hạn đếm được

Với 3 giả thiết trên thì việc xác định số nguyên tố lớn nhất là không thể được; tuy nhiên, với khả năng tính toán của máy tính, người ta có thể tính ra được số nguyên tố (số nguyên chắc chắn là số nguyên tố) lớn nhất tính được đến tháng 9 năm 2008 là số nguyên tố Mersenne thứ 45 (hay 46 nếu tính cả số 1) với 12,978,189 chữ số:

2^43,112,609 − 1..

(theo http://vi.wikipedia.org)