Một số dạng toán về mặt phẳng & đường thẳng – Thầy Đồ – Dạy toán

MỘT SỐ DẠNG TOÁN THƯỜNG GẶP

Dạng 1: Viết phương trình tham số và phương trình chính tắc của đường thẳng $\Delta$

Phương pháp :

Xác định một điểm cố định $M_0 (x_0 ;y_0 ;z_0 )$ $\in$ $\Delta$

Xác định một vectơ chỉ phương $\overrightarrow a=(a_1;a_2;a_3)$ của $\Delta$ .

Phương trình tham số và phương trình chính tắc của $\Delta$ lần lượt có dạng

$\Delta$ : $\left\{ \begin{array}{l} x=x_0+a_1 t \\ y=y_0+a_2t \\ z=z_0+a_3t \end{array} \right.$

$\Delta$ : $\frac{{x - x_0 }}{{a_1 }}=\frac{{y - y_0 }}{{a_2 }} = \frac{{z - z_0 }}{{a_3 }}$ nếu $a_1;a_2;a_3$ đều $\ne 0$

Ví dụ : Viết phương trình tham số và phương trình chính tắc của đường thẳng $\Delta$ đi qua hai điêm $A(1;2;3$ và $B(4;5;6)$

Lời giải:

$\Delta$ đi qua hai điểm $A(1;2;3$ và $B(4;5;6)$ nên có vectơ chỉ phương $\overrightarrow {AB}=(3;3;3)$

Vậy phương trình tham số của $\Delta$ là: $\left\{ \begin{array}{l} x=1+3t \\ y=2+3t \\ z=3+3t \end{array}\right.$

Vậy phương trình chính tắc của $\Delta$ là: $\frac{x - 1}{3}=\frac{y - 2}{3}=\frac{z - 3}{3}$

Dạng 2: Vị trí tương đối giữa hai đường thẳng $\Delta$ và $\Delta'$ trong không gian.

Phương pháp :

Xác định điểm cố định $M_0 (x_0 ;y_0 ;z_0 )$ và vectơ chỉ phương $\overrightarrow a=(a_1;a_2;a_3)$ của $\Delta$ .Xác định điểm cố định $M_0 (x'_0 ;y'_0 ;z'_0)$ và vectơ chỉ phương $\overrightarrow a'=(a'_1;a'_2;a'_3)$ của $\Delta'$ .

Tính $\overrightarrow n=[\overrightarrow a ;\overrightarrow {a'}]$ .

Dùng các dấu hiệu sau để xét vị trí tương đối giữa $\Delta$ và $\Delta'$ .

$\Delta$ // $\Delta'$ $\Leftrightarrow$ $\left\{ \begin{array}{l} \overrightarrow{n}=\overrightarrow{0} \\ M_{0}\notin \Delta' \end{array}\right.$

$\Delta$ $\equiv$ $\Delta'$ $\Leftrightarrow$ $\left\{ \begin{array}{l} \overrightarrow{n}=\overrightarrow{0} \\ M_{0}\in \Delta' \end{array}\right.$

$\Delta$ cắt $\Delta'$ $\Leftrightarrow$ $\left\{ \begin{array}{l} \overrightarrow{n}\ne \overrightarrow{0} \\ \overrightarrow{n}\overrightarrow{M_0M_0'}=0 \\ \end{array}\right.$

$\Delta$ và $\Delta'$ chéo nhau $\Leftrightarrow$ $\overrightarrow n.\overrightarrow{M_0 M_0 '}\ne 0$

Ví dụ: Xét vị trí tương đối của đường thẳng $\Delta$ là: $\frac{x - 1}{2}=\frac{y+2}{3}=\frac{z - 5}{1}$ với đường thẳng

$d$ : $\left\{\begin{array}{l} x=3+4t \\ y=2+3t \\ z=6+5t \end{array}\right.$

Lời giải:

Ta có đường thẳng $\Delta$ đi qua điểm $M_0(1; - 2;5)$ và có vectơ chỉ phương $\overrightarrow a=(2;3;1)$
$d$ đi qua $M(3;2;6)$ và có vectơ chỉ phương $\overrightarrow a=(4;3;5)$

Ta có : $\overrightarrow n=[\overrightarrow a ;\overrightarrow {a'}]=(12;-6;-6)$ $\ne \overrightarrow 0$ .

$\overrightarrow{M_0M}=(2;4;1)$

$\overrightarrow {n.} \overrightarrow{M_0 M}=24-24-6=-6$

Vậy $\Delta$ và $d$ chéo nhau.

Các em có thể lấy ví dụ về các trường hợp còn lại

Dạng 3: Vị trí tương đối giữa đường thẳng và mặt phẳng.

Phương pháp :

Cho đường thẳng $d$ đi qua điểm $M_0(x_0 ;y_0 ;z_0 )$ và vectơ chỉ phương $\overrightarrow a=(a_1;a_2;a_3)$ , cho mặt phẳng $( \alpha)$ có phương trình tổng quát $Ax+By+Cz+D=0$ .

Gọi $\overrightarrow n=(A;B;C)$ là VTPT của $(\alpha)$ .

Để xét vị trí tương đối giữa đường thẳng $d$ và mặt phẳng $(\alpha)$ ta có các cách sau:

Cách 1: Xét tích vô hướng $\overrightarrow n.\overrightarrow a$ và thay tọa độ của điểm $M_0$ vào phương trình của $( \alpha)$ để kiểm tra , ta có các trường hợp sau:

$\left\{\begin{array}{l} \overrightarrow{n}.\overrightarrow{a}=0 \\ M_{0}\notin (\alpha) \end{array}\right.$ $\Leftrightarrow$ $d$ song song với $( \alpha)$ .

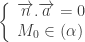
$\left\{\begin{array}{l} \overrightarrow{n}.\overrightarrow{a}=0 \\ M_{0} \in (\alpha) \end{array}\right.$ $\Leftrightarrow$ $d$ nằm trong $( \alpha)$ .

$\overrightarrow n.\overrightarrow a\ne 0$ $d$ cắt $(\alpha)$ .

$\overrightarrow n=k\overrightarrow a$ $\Leftrightarrow$ $d$ vuông góc với $(\alpha)$ .

Cách 2: Viết phương trình tham số của đường thẳng $d$ : $\left\{ \begin{array}{l} x=x_0+a_1 t \\ y=y_0+a_2t \\ z=z_0+a_3t \end{array} \right.$

Sau đó thay $x,y,z$ ở phương trình tham số trên vào phương trình tổng quát của mặt phẳng $( \alpha)$ : $Ax+By+Cz+D=0$ ta được:

$A(x_0+a_1 t)+B(y_0+a_2t)+C(z_0+a_3t)+D=0$ hay $mt+n=0$ (1)

Xét số nghiệm $t$ của phương trình (1) ta có các trường hợp sau.

$(1)$ vô nghiệm $\Leftrightarrow$ $d$ song song với $( \alpha)$ .

$(1)$ có mộy nghiệm $t=t_0$ $\Leftrightarrow$ $d$ cắt $( \alpha)$ tại điểm $M_0(x_0+a_1 t;y_0+a_2t;z_0+a_3t)$

$(1)$ có vô số nghiệm $\Leftrightarrow$ $d$ nằm trong $( \alpha)$ .

$(1)$ $(A;B;C)=k(a_1;a_2;a_3)$ $\Leftrightarrow$ $d$ vuông góc với $( \alpha)$ .

Ví dụ: Xét vị trí tương đối của đường thẳng $\Delta$ là: $\frac{x-1}{2}=\frac{y+2}{3}=\frac{z-5}{1}$ với mặt phẳng $( \alpha)$ : $x-y+2z+5=0$

Lời giải:

Chuyển phương trình chính tắc của $\Delta$ về phương trình tham số

$\Delta$ : $\left\{ \begin{array}{l} x=1+2t \\ y=-2+3t \\ x=5+t \end{array} \right.$

Sau đó thay $x,y,z$ ở phương trình tham số trên vào phương trình tổng quát của mặt phẳng $( \alpha)$ : $1+2t-(-2+3t)+2(5+t)+5=0$ $(1)$

$\Leftrightarrow$ $t=-18$

Phương trình $(1)$ có một nghiệm $t=-18$ , vậy $\Delta$ cắt $( \alpha)$ tại điểm $M_0(-35;-56;-13)$

Dạng 4: Tìm hình chiếu.

Bài toán 1: Tìm hình chiếu vuông góc $H$ của điểm $A$ trên đường thẳng $(d)$ .

Phương pháp:

Viết ptmp (P) qua A vuông góc (d)
thay PTTS (d) vào (P) tìm t=?
thay t vào PTTS (d) tìm được 3 tọa độ đó là H.

Bài toán 2: Tìm hình chiếu vuông góc $H$ của điểm $A$ trên mặt phẳng $( \alpha)$ .Cách 1: Gọi $H(x;y;z)$

$H \in (\alpha)$ (*)

$\overrightarrow {AH}$ cùng phương với $\overrightarrow {n_\alpha}$ : Biến đổi tỉ lệ thức này để dùng điều kiện (*) ,từ đó tìm được $x;y;z$ .

Cách 2:

Tìm phương trình ts đường thẳng $(d)$ đi qua $A$ và vuông góc với mặt phẳng $( \alpha)$ .

Giao điểm của $(d)$ và $( \alpha)$ chính là hình chiếu $H$ của $A$ trên mặt phẳng $( \alpha)$ .

Bài toán 3: Tìm hình chiếu vuông góc $(\Delta)$ của đường thẳng $(d)$ xuống mặt phẳng $( \alpha)$ .

Tìm phương trình mặt phẳng $(\beta)$ chứa đường thẳng $d$ và vuông góc với mặt phẳng $( \alpha)$ .

Hình chiếu $(\Delta)$ của $(d)$ xuống mặt phẳng $( \alpha)$ chính là giao tuyến của $( \alpha)$ và $(\beta)$ .

Thí dụ: Cho hai điểm $A(-1;3;-2),B(-9;4;9)$ và mặt phẳng $(P):2x-y+z+1=0$ . Tìm điểm $M\in(P)$ sao cho $AM+BM$ là nhỏ nhất.

Hướng dẩn giải:

Đặt $f(x;y;z)=2x-y+z+1$ .

Ta có $f(-1;3;-2)=-6<0$

$f(-9;4;9)=-12<0$

Vậy $A,B$ về cùng một phía của $(P)$

Gọi $A_1$ là điểm đối xứng của $A$ qua $(P)$

Nối $BA_1$ , Ta có ${BA_1}\cap (P)=M$

Khi đó dễ chứng minh $M$ chính là điểm cần tìm( Bài toán cơ bản của phép tính đối xứng qua mặt phẳng )

Gọi $A'$ là hình chiếu của $A$ trên $(P)$

Đường thẳng $AA'$ có dạng $\left\{ \begin{array}{l} x=-1+2t \\ y=3-t \\ z=-2+t \end{array}\right.$

Gọi $A'(-1+2t;3-t;-2+t)$

Ta có phương trình sau để xác định t (dựa vào $A' \in (P)$ :

$2(-1+2t)-(3-t)+(-2+t)+1=0$ $\Leftrightarrow$ $6t-6=0$ $\Leftrightarrow$ $t=1$

Vậy $A'(1;2;-1)$ . Do $A'$ là trung điểm của $AA_1$ , nên có ngay $A_1(3;1;0)$ .

Ta có $\overrightarrow{BA_1}(12;-3;-9)$ cùng phương với vectơ $(4;-1;-3)$

Vậy $BA_1$ có dạng $\left\{\begin{array}{l} x=3+4t \\ y=1-t \\ z=-3t \end{array} \right.$

Giả sử $M(3+4t';1-t';-3t')$ , khi đó ta có phương trình sau để xác định t’(dựa vào $M \in (P)$ :

$2(3+4t')-(1-t')-3t'+1=0$

Vậy $M(-1;2;3)$ là điểm cần tìm

Chú ý: Nếu $A,B$ ở hai phía của $(P)$ , thì nếu gọi $M = AB \cap (P)$ , Thì $M$ chính là điểm cần tìm.

(sưu tầm)