Pierre de Fermat (1601 – 1665) – Thầy Đồ – Dạy toán

Pierre de Fermat (20 tháng 8, 1601 tại Pháp – 1665) là một học giả nghiệp dư vĩ đại, một nhà toán học nổi tiếng và cha đẻ của lý thuyết số hiện đại. Xuất thân từ một gia đình khá giả, ông học ở Toulouse và lấy bằng cử nhân luật dân sự rồi làm chánh án. Chỉ trừ gia đình và bạn bè tâm giao, chẳng ai biết ông vô cùng say mê toán. Mãi sau khi Pierre de Fermat mất, người con trai mới in dần các công trình của cha kể từ năm 1670. Năm 1896, hầu hết các tác phẩm của Fermat được ấn hành thành 4 tập dày. Qua đó, người đời vô cùng ngạc nhiên và khâm phục trước sức đóng góp dồi dào của ông. Chính ông là người sáng lập lý thuyết số hiện đại, trong đó có 2 định lý nổi bật: định lý nhỏ Fermat và định lý lớn Fermat (định lý cuối cùng của Fermat).

Trong hình học, ông phát triển phương pháp tọa độ, lập phương trình đường thẳng và các đường cong bậc hai rồi chứng minh rằng các đường cong nọ chính là các thiết diện cônic. Trong giải tích, ông nêu các quy tắc lấy đạo hàm của hàm mũ với số mũ tỷ bất kỳ, tìm cực trị, tính tích phân những hàm mũ với số mũ phân số và số mũ âm. Nguyên lý Fermat về truyền sáng lại là một định luật quan trọng của quang học.

Dù hoạt động khoa học kiên trì và giàu nhiệt huyết, đem lại nhiều thành quả to lớn như vậy, nhưng éo le thay, Pierre de Fermat bình sinh chẳng thể lấy việc nghiên cứu toán làm nghề chính thức.

Định lý nhỏ Fermat

Với p là một số nguyên tố khác 2 thì chia một số a lũy thừa p cho p sẽ có số dư chính bằng a:

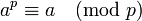
$a^p \equiv a \pmod{p}\,$

Định lý lớn Fermat

Câu chuyện về định lý cuối cùng của Fermat là câu chuyện độc nhất vô nhị trong lịch sử toán học thế giới, khởi nguồn từ cổ đại với nhà toán học Pythagore. Bài toán cuối cùng (sau này giới toán học gọi là Định lý cuối cùng của Fermat, hay Định lý lớn Fermat) có gốc từ định lý Pythagore: “Trong một tam giác vuông, bình phương cạnh huyền bằng tổng bình phương hai cạnh góc vuông”. Fermat thay đổi phương trình Pythagore và tạo ra một bài toán khó bất hủ.

Xét phương trình Pythagore:

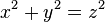
$x^2 + y^2 = z^2\,$

Người ta có thể hỏi những nghiệm số nguyên của phương trình này là gì, và có thể thấy rằng:

$3^2 + 4^2 = 5^2\,$

và

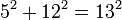
$5^2 + 12^2 = 13^2\,$
Nếu tiếp tục tìm kiếm thì sẽ tìm thấy rất nhiều nghiệm như vậy. Fermat khi đó xét dạng bậc ba của phương trình này:

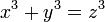
$x^3 + y^3 = z^3\,$

Ông đặt câu hỏi: có thể tìm được nghiệm (nguyên) cho phương trình bậc ba này hay không? Ông khẳng định là không. Thực ra, ông khẳng định điều đó cho họ phương trình tổng quát:

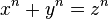
$x^n + y^n = z^n\,$

trong đó n lớn hơn 2 không thể tìm được nghiệm (nguyên) nào. Đó là Định lý Fermat cuối cùng.

Điều lý thú ở đây là phỏng đoán này được Fermat ghi bên lề một cuốn sách mà không chứng minh, nhưng có kèm theo dòng chữ: “Tôi có một phương pháp rất hay để chứng minh cho trường hợp tổng quát, nhưng không thể viết ra đây vì lề sách quá hẹp.”!!

Các nhà toán học đã cố gắng giải bài toán này trong suốt 300 năm. Trong lịch sử đi tìm lời giải cho định lý cuối cùng của Fermat có người phải tự tử và có cả sự lường gạt… Và cuối cùng nhà toán học Andrew Wiles (một người Anh, định cư ở Mỹ, sinh 1953) sau 7 năm làm việc trong cô độc và 1 năm giày vò trong cô đơn đã công bố lời giải độc nhất vô nhị vào mùa hè năm 1993 và sửa lại năm 1995, với lời giải dài 200 trang. (Nguồn vi.wikipedia.org)