Mẹo tính nhanh tích phân từng phần – Thầy Đồ – Dạy toán

Trước tiên, ta nhắc lại một chút về kiến thức của phép lấy tích phân theo từng phần:

Giả sử u và v là hai hàm số khả vi của x. Khi đó, như ta đã biết, vi phân của tích uv được tính theo công thức:

$d(uv) = udv + vdu$

Từ đó, lấy tích phân ta được:

$uv = \int {udv} + \int {vdu}$

Hay là:

$\int {udv} = uv - \int {vdu}$ (1)

Công thức này gọi là công thứclấy tích phân từng phần. Công thức này thường được dùng để lấy tích phân các bểu thức có thể biểu diễn dưới dạng tích của hai nhân tử u và dv, sao cho việc tìm hàm số v theo vi phân dv của nó và việc tính tích phân $\int {vdu}$ là những bài toán đơn giản hơn so với việc tính trực tếp tích phân $\int {udv}$ . Ý nghĩa tách biểu thức dưới dấu tích phân thành các thừa số u và dv thường xảy ra trong quá trình giải các bài toán có dạng sau:

$\int {P_{n}(x).sinaxdx} , \int {P_{n}(x).cosaxdx} , \int {P_{n}(x).e^{ax}dx} , \int {P_{n}(x).lnxdx}$

trong đó P_n là đa thức bậc n.

Với các dạng trên, thì thông thường vai trò của u luôn là đa thức P_n , và dv là phần còn lại. Như vậy, ta có sơ đồ sau:

Khi được tích phân mới, ta lại được một tích phân lại là một trong các dạng, và phần đa thức mới lại đóng vai trò là u, còn phần còn lại tiếp tục đóng vai trò là v…. Cứ thế cho đến khi bậc của đa thức là bậc 0 thì sẽ có kết quả. Như vậy, các đa thức luôn đóng vai trò u (nghĩa là lấy đạo hàm), còn phần cò lại luôn là dv (lấy tích phân), nên ta sẽ xây dựng thật toán gồm 2 cột: 1 cột chuyên lấy đạo hàm của đa thức cho đến khi giá trị bằng ; 1 cột luôn lấy tích phân tương ứng với cột kia. Sau đó, ghép các giá trị uv lại ta sẽ có kết quả. Hay ta có sơ đồ sau:

Ví dụ: Cần tính $\int {(x^2 + 7x - 5).cos2x dx}$

Ta lập sơ đồ như sau:

Khi đó, kết quả của tích phân này sẽ là:

$(x^2+7x-5) { \frac{sin2x}{2}}+(2x+7) { \frac{cos2x}{4}} - { \frac{sin2x}{4}}$

Ví dụ 2: Cần tính: $\int {(x^3 + 4x^2 - 5x + 6).e^{-x} dx}$

Ta có sơ đồ sau:

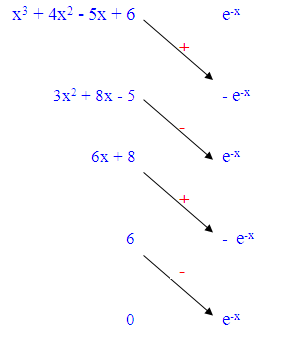
Vậy, dựa vào sơ đồ trên, ta có kết quả của bài toán là:

$- {(x^3+4x^2-5x+6)e^{-x} }-{(3x^2+8x-5)e^{-x}}-{(6x+8)e^{-x}}-6e^{-x}$

Hay:

$- (x^3 + 7x^2 + 9x + 15)e^{-x}$

Tóm lại, qua sơ đồ thuật toán và 2 ví dụ vừa trình bày, chúng tôi hy vọng đã cung cấp cho các bạn một chiêu giúp chúng ta tính kết quả của các tích phân từng phần một cách nhanh chóng, và hiệu quả mà không cần phải đặt u, v lòng vòng như sách giáo khoa đã trình bày.

(Theo http://thunhan.wordpress.com)