I) Fractal là gì?
1) Vì sao phải là đường thẳng?
2) Vì sao phải là hình vuông?
3) Vì sao phải là những hình đối xứng?
…
Từ những câu hỏi đó Mandelbrot đã đưa ra một thứ hình học đẹp tuyệt vời, đó là fractal. Môn hình học miêu tả xác thực cuộc sống hơn hình học Ơclit. Thế fractal là gì?
Có thể định nghĩa một cách nôm na với fractal không ngẫu nhiên như sau (nghĩa là có cái ngẫu nhiên). Những đối tượng hình học nằm trên đường thẳng, mặt phẳng, không gian có tính chất tự đồng dạng. Được gọi là fractal.
Có thể giải thích là, những đối tượng hình học được xây dựng bằng những quy tắt nào đó. Để hiểu rõ hơn, ta đưa ra một vài ví dụ
II) Ví dụ
1) Tập Cantor
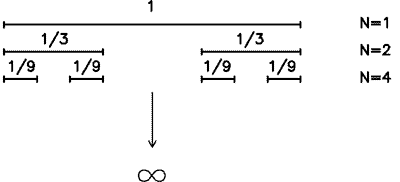
Xét đoạn thẳng có độ dài bằng 1. Ta thực hiện theo quy tắc sau.
i) Chia thành ba phần đều nhau, và bỏ đi phần hai ( phần giữa)
ii) Hai phần 1 và 3 thực hiện theo bước i)
Quy tắc được mô tả bởi hình ảnh sau
2) Bông tuyết Koch
Được mô tả bằng hình ảnh sau


Ta nhận được bông tuyết Koch sau

3) Tam giác Sierpinski
Được thực hiện theo hình ảnh sau

Ta nhận được tam giác Sierpinski sau:

Ngoài fractal không ngẫu nhiên còn có một fractal ngẫu nhiên. Fractal ngẫu nhiên chỉ khác fractal không ngẫu nhiên một đều đó là các quy tắc thực hiện cũng một cách ngẫu nhiên. Ví dụ trong tập Cantor, ta không xóa đi phần giữa, mà xóa đi một phần ngẫu nhiên. Có thể là, gieo con xúc sắc nếu rơi 1 hoặc 2 chấm thì có thể bỏ đi phần 1. Nếu xuất hiện 3,4 thì ta bở đi phần 2. Còn nếu xuất hiện 5,6 thì bỏ đi phần 3.
Hiện nay, môn hình học này có rất nhiều ứng dụng trong khoa học cũng như trong cuộc sống. Mời các bạn cùng trao đổi về thứ tuyệt đẹp xa xỉ này!!!
Sau đây là một số hình tuyệt đẹp. Có những hình rất gần gũi với cuộc sống. Mời các bạn thưởng thức






Cõ lẽ trong lịch sử phát triển của toán chưa có một môn hoc nào huyền bí và lãng mạn đến vậy… trong bài viết này tôi sẽ không nhắc nhiều nữa những ứng dụng to lớn của môn học này mà chỉ nêu lên một số câu hỏi nho nhỏ.
Có lẽ ai trong chúng ta cũng quen với số , vậy
là gì? ko phải ngẫu nhiên trong toán học nảy sinh ra số
để rồi ngày nay ta dùng nó. Nói đến số
người ta ko thể ko nhắc đến hình tròn, và hình tròn nó chứa đựng cho mình một tính chất rất lạ: độ dài đường tròn lớn hơn đường kính của nó một số lần ko fụ thuộc vào bản thân hình tròn đó? Tại sao các hình tròn lại giống nhau?…và còn nhiều nữa các câu hỏi cứ ám ảnh những ai đam mê hình học Ơclit…
Nhưng có một câu hỏi làm điên đảo nhiều người nhất đó là: “Liệu có tồn tại một đối tượng có chiều là “. Nếu chúng ta hiểu khái niệm chiều một cách thô sơ nhất đó là số toạ độ ít nhất dùng để xác định vị trí duy nhất của một điểm trong không gian thì hiển nhiên số chiều fải là tự nhiên, và đáp án cho cái câu hỏi ngớ ngẩn trên đương nhiên là ko có. Nhưng có một khái niệm chiều suy rộng khác ( giả sử định nghĩa của nhàtoán học Đức Hausdorf) chiều được cho bởi công thức
và khi đó cái câu hỏi ngớ ngấn trên ko còn tầm thường nữa: Có tồn tại các số tự nhiên
sao cho
? vẫn là một câu hỏi hóc búa…
Một câu hỏi khác cũng ko kém tính thời sự đó là “có tồn tại số tự nhiên n sao cho ”
Đó là những điều thú vị cho những ai hướng đến thế giới fractal kì diệu!
Mời các bạn ghé thăm trang sau để cảm nhận sự lung linh huyền ảo thật sự của Fractal…
http://www.allisonart.com/index.html
(Nguồn mathvn.org)